ThreeB 1.1
3B Microscopy Analysis

Introduction

This project contains the reference implementation of the 3B microscopy analysis method, and an ImageJ plugin. Please refer to the project website for more information on the method.

To get started with analysing data, the ImageJ plugin is the most suitable piece of software. This can be obtained from the the project website.

For more advanced analysis (such as running on a cluster), the the program multispot5_headless should be used. This program needs to be run from the commandline.

This project contains the source code for the commandline program and the ImageJ plugin.

Getting started

Dataset types and experimental parameters

Bayesian analysis of blinking and bleaching allows data to be extracted from datasets in which multiple fluorophores are overlapping in each frame. It can of course also be used to analyse standard localisation (PALM/STORM) data, but it must be borne in mind that the low density and high frame number of such datasets can lead to long runtimes. Here we briefly discuss the different types of dataset, related to different applications, that you may wish to analyse using 3B.

Low density PALM/STORM datasets

These datasets have few fluorophores overlapping in each image and are at least 10,000 frames long. As discussed above, they can be analysed with 3B but their run time makes this a large time investment. If you wish to use this approach for performance verification, we would suggest selecting a small spatial area (around 1.5-3 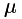$\mu$m square). The algorithm can also be parallelised by running different sets of a few hundred frames for the same area separately. Even with parallelisation, the large number of frames will make it time consuming to run. If you simply want to know what the structure is like, we would suggest using a method such as QuickPALM, which are very fast in comparison.

High density fixed cell datasets

These datasets are of fixed cells but have multiple fluorophores overlapping in each frame. You may acquire this type of dataset if the system you use has a fluorophore which cannot be photoswitched, or the blinking properties of which cannot be tuned over a wide enough range using the embedding medium, or if your light source is not powerful enough to drive most of the fluorophores into the non-emitting state. In fixed samples labelled with fluorescent proteins there will in our experience be almost no blinking present, and 3B will therefore pick up bleaching. While this can produce satisfactory results, the localisation is on single event on a high background and therefore the performance will be significantly degraded.

Some users choose to acquire this type of dense data if they have severe problems with drift, particularly in the z-direction, as it drastically cuts the drift over the acquisition time. However, in the long term it is worth trying to improve the stability of such systems, since z-drift will impact the accuracy of all types of localisation measurement. If you are unsure how badly your system is affected by z-drift, it is useful to carry out a calibration of the drift of the microscope using a bead sample before starting acquisition of data for superresolution.

Live cell datasets

These datasets are of live cells, generally labelled with standard fluorescent proteins such as mCherry. The mounting medium should be phenol red free, to avoid unnecessary background. The intensity of the light source should be selected such that it is high enough to produce blinking but not strong enough to completely bleach the sample over the time of the acquisition. For example, for a standard Xe arc lamp illumination with the full power of the lamp is generally suitable, but if you are using a powerful laser source it is recommended to take multiple datasets with different power levels to determine which is suitable.

The time which is needed to acquire the data necessary for a single superresolution frame is dependent on the illumination intensity, the speed of the camera, and the properties of the flurophore. Many older EMCCD cameras have a maximum acquisition speed of around 50 frames per second for a small region of interest, which then gives a limit of 4 s to acquire 200 frames. High specification EMCCD cameras and SCMOS cameras have much higher acquisition speeds of up to thousands of frames per second for restricted areas. However, in order to maintain the number of photons from each flurophore per frame the illumination intensity would have to be increased, which is likely to bleach the sample rapidly, and change the blinking properties of the fluorophore to some extent.

The acquisition of live cell datasets allows dynamics to be observed. It should be noted, however, that if the structures move over the timescale of the acquisition then that movement will cause blurring in the reconstructed image.

Live cell datasets

The 3B algorithm must be able to pick up the changes in intensity which occur when a fluorophore switches between an emitting and a non-emitting state. The accuracy with which localisation can occur depends, as for other localisation techniques, on the number of photons from the fluorophore and the background level. Since 3B is generally used with a widefield setup, if the sample has a lot of fluorescent structure out of the plane of focus, the background will be higher and it will be more difficult to localise. For thick samples, the background can be reduced by using TIRF or high angle illumination.

Iterations and run time

In general, determining the number of iterations required for MCMC algorithms is an unsolved problem. A good general rule is that once the reconstruction stops changing significantly with increasing iterations, then it is likely that the reconstruction has converged to a reasonable point.

If you are unsure, then rerun exactly the same area with exactly the same parameters, but with a different random seed. Note that the ImageJ plugin will automatically select a different seed each time in the standard interface, but with the advanced interface or commandline program, the seed must be specified in the configuration file (see The configuration file and advanced settings). If the two results appear essentially the same, then it is very likely that a sufficient number of iterations has been reached.

A good general rule is that 200 iterations is sufficient for convergence under almost all circumstances. For the example usage given in this manual, the required number of iterations for good convergence requires about 6 hours on a standard PC (Core i7 at 3GHz).

Convergence may be achieved before 200 iterations, but terminating the run before convergence can lead to artefacts. As with any microscopy method, the experiment and analysis should always be carried out appropriately to minimise the risk of artefacts.

There are a number of issues which can lead to artefacts:

Using the ImageJ Plugin

A tutorial for using the ImageJ plugin is provided under Plugins>3B>Help

The plugin can operate in two modes, standard and advanced. The standard mode allows the user to set the microscope PSF and spot size, the starting number of spots for the analysis and the range of frames.

The plugin also offers an advanced mode of operation which allows much greater control over 3B. See The configuration file and advanced settings for further details.

Using the commandline program

We have provided a set of test data on the website. Download and unpack the zip file. It will create a new directory called test data with the collowing contents: 

test_data/AVG_test_data.bmp
test_data/markup1.bmp
img_000000000.fits
img_000000001.fits
img_000000002.fits
...
img_000000299.fits

Then run the following command:

./multispot5_headless --save_spots test_data/results.txt --log_ratios test_data/markup1.bmp test_data/img_000000*

The program will save the results in the file test_data/results.txt . The program will run indefinitely in the default setup, but you may view the results at any stage. There is no well defined stopping point for this type of algorithm, so it is advisable continuously monitor the resultant image, and stop the algorithm when the output image is no longer changing with time. After 30 minutes on a fast PC (e.g. Core i7 975), the ring structure which is not resolved in the widefield image should be clearly visible. After about 75 mins, the finer details of the structure begin to approach those seen in Fig 2e in the associated paper.

The ImageJ plugin can load a results file and perform a reconstruction.

Alternatively, you can process the results file further in order to view the results. Run the following command: 

awk '/PASS/{for(i=2; i <=NF; i+=4)print $(i+2), $(i+3)}' test_data/results.txt > test_data/coordinates.txt

The file test_data/coordinates.txt contains a long list of 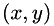$(x, y)$ coordinates, representing possible spots positions. In order to view the results, load the data into a graph plotting program and create a scatter plot. NOTE: the axes are in pixel coordinates, so you will have to multiple any distances by the number of nm/pixel in order to get distances in nm.

Example usage explained

Test Data

The 300 TIFF files in the test directory correspond to the data used for Fig. 2 in the paper. Please refer to the paper for details on how the data was obtained.

The file AVG_test_data.bmp is a Z projection made using ImageJ.

The file markup1.bmp is a mask indicating which area of the image to analyse. All perfectly black pixels are ignored, ecerything else is analysed. If you overlay markup1.bmp and AVG_test_data.bmp you can see which area the markup corresponds to. The markup file was created using the GIMP.

Running the program

The general form for running the program is:

./multispot5_headless [ --variable1 value1 [ --variable2 value 2 [ ... ] ] ] image1 image2 ...

so the example sets ths variable save_spots to test_data/results.txt and the variable log_ratios to test_data/markup1.bmp. The remaining arguments is the list of files to be analysed.

The program gets the markup in the filename given in the log_ratios variable (yes, the choice of name is very strange, and corresponds to a very old phase of development). The more sanely named variable save_spots is the filename in which the output is to be saved.

The program actually has a large number of variables which must be set. Most of them you probably don't want to change, but some of them you will want to change. The default values for these variables are stored in multispot5.cfg The format of this file should be mostly self explanatory. Everything after a is a comment and is ignored. See The configuration file and advanced settings for further details.

You will probably want to change:

Note that variables specified on the commandline override all variables in the configuration file.

The program can read FITS, BMP, PPM and PGM images. Depending on how it has been compiled, it can also read TIFF, PNG and JPEG images. The program cannot work on multi-image TIFF files. ImageJ can be used to split a multi-image TIFF into a collection of single image files. All the images loaded must be the same size.

Extracting and visualising the data

The output file (in this case test_data/results.txt ) containing the results is in a format unsuitable for plotting directly, and must be extracted. The reason for this is that the output file contains enough information to seamlessly continue long runs which have been interrupted. The provided AWK program extracts the coordinates of the spots over all iterations and puts them in coordinates.txt.

Alternatively, the data can ve visualised using the plugin under the menu Plugins>3B>Open 3B run

The configuration file and advanced settings

The 3B system has a large number of parameters which control its behaviour. These are controled via the configuration file for the commandlie program or via the ``Advanced'' option for the plugin. The ``Advanced'' option essentially allows you to supply a fully custom configuration file.

The sample configuration file is given below along with explanations of all parameters. In the program, most of these parameters are used by the FitSpots class.

////////////////////////////////////////////////////////////////////////////////
//
// Advanced setting.
//
// You probably do not want to change most of these.
//
// Parameters which you are most likely to need to change are marked 
// CHANGE THIS
//
// Note that if a variable is set twice, the last setting takes precedence.
//
// Comments in this section should be read in conjunction with the paper, 
// online methods and supplementary material.
//
// Any line starting with // is a comment and is ignored by the
// plugin.


////////////////////////////////////////////////////////////////////////////////
//
// Things you might want to change are below here
//

//Random seed for the Monte-Carlo process.
//Changing this value will change the random numbers which are generated.
//Please refer to the user manual section "Iterations and run time" for
//further discussion.
seed=0

////////////////////////////////////////////
//
// Spot intensity priors. You can probably leave this as-is unless your
// fluorophores are very much brighter compared to the noise than the ones
// in the paper. See "Modelling the image" in Supplementary Note 1.
//
// See here for definitions of mu and sigma:
// http://en.wikipedia.org/wiki/Log-normal_distribution
//
// Note that these values are for the spot brightness once the image
// has been normalised to have unit standard deviation so these should
// not be changed unless your images are very significantly less noisy
// than the data presented in the paper.
//
intensity.rel_mu=2
intensity.rel_sigma=1


////////////////////////////////////////////
//
// Spot shape priors. CHANGE THIS
//
// This specifies the log-normal distribution for the prior over spot
// radius. This is specified in pixels, not nm.

//Corresponds to 300nm at 100nm per pixel
blur.mu=0.242
blur.sigma=0.1

//Corresponds to 300nm at 160nm per pixel
blur.mu=-0.218
blur.sigma=0.1

//Corresponds to 270nm at 79nm per pixel
//blur.mu=0.37261
//blur.sigma=0.1


//Number of spots. CHANGE THIS
//
//15 is suitable for a small image patch, such as the example in the
//help menu.
//
//If you set this too high, the system will run very slowly.
placement.uniform.num_spots=15



////////////////////////////////////////////////////////////////////////////////
//
// You probably do not want to change anything below here.
//


//Transition matrix and initial probabilities

// Following the notation in [24], A represents the transition
// probabilities of the HMM and pi the initial state. A corresponds
// to Supplementary Figure 4 as:
//    A = [ P1 P2 0; P3 P4 P5; 0 0 1]
// These are used in the inner integral of eq 7.

A=[0.16 0.84 0; 0.495 0.495 0.01; 0 0 1]
pi=[.5 .5 0]



//////////////////////////////////////////////////
//
//General parameters

// All MCMC systems can use mixing samples[28], which are drawn by
// by the sampler but do not take part in further computations. 
// For every mixing_iterations samples drawn 1 is uses, so
// mixing_iterations=1 corresponds to no mixing.

//Number of mixing iterations used by all Gibbs samplers in this algorithm.
gibbs.mixing_iterations=1



//////////////////////////////////////////////////
//
//Specific subsystem parameters


////////////////////////////////////////
//
// Main optimization - step 2 of the algorithm

//maximum l_inf of motion vector during optimization stage.
//See step 2 of the algorithm,
cg.max_motion=0.5

//Scale the maximum step in brightness according to the prior shape
//The reason is that the brightness is a very different scale from
//the spot position and shape, so the optimizer will get stuck
//taking many tiny steps in the direction of brightness.
//
//If this is set to 0 then no scaling is used.
//
//If it is set to 1, then scale by the brighness step by the standard
//deviation of the prior distribution.
max_motion.use_brightness_std=1

//Maximum number of iterations of conjugate gradient optimization
//See [29] for a description of an iteration in this context.
main.cg.max_iterations=5

//Number of samples used for computing gradient using hybrid method.
//This corresponds to S, as applied to step 2 of the algorithm.
main.gibbs.samples=10

//Number of passes of optimization in step 2 to be completed before
//advancing to step 3.
main.passes=4


//Allow spots to be at most this far outside the marked region
//Anything further outside will be removed automatically.
position.extra_radius=2.3

////////////////////////////////////////
//
// Add/remove spots - step 3 of the algorithm

//When computing Z, in step 3a and 3c, use a uniform position prior (to
//make spot probability a proper distribution). If this is set to 0, then
//no position prior is used. Do not set to 0 except for debugging.
position.use_prior=1

//Number of samples used to compute the gradient usint the 
//hybrid method, as applied to step 3c.
add_remove.optimizer.samples=20

//The optimizer can get stuck on saddle points. If a saddle point
//is found, the the optimizer will restart in the direction corresponding
//to the worst eigen value. Up to this many restarts will be attempted before
//gving up. Step 3c.
add_remove.optimizer.attempts=10

//There is no efficient algorithm for evaluating the Hessian (equivalent
//to the inner integral in Eq 6, but for second derivatives). The integral 
//is approximated using Monte-Carlo integration (note, not MCMC), with this
//many samples drawn from the Markov chain using FFBS.
//
//The outer summation uses add_remove.optimizer.samples samples.
add_remove.optimizer.hessian_inner_samples=1000

//Number of cycles of thermodynamic integration  (step 3a and 3c) and 
//eq 2.
//Note that the equation 1.25^(i/10) only applies if this number is set 
//to 1000 as it was for all experiemnts in the paper. The actual equation is:
//1.25^(100 * i/add_remove.thermo.samples)
add_remove.thermo.samples=1000

//Outer and inner samples for computing the Hessian using the hybrid method
//in step 3e.
//
//See add_remove.optimizer.hessian_inner_samples for an explanation of the
//meaning.
add_remove.hessian.outer_samples=100
add_remove.hessian.inner_samples=1000

//Number of repeats of step 3.
add_remove.tries=10


//////////////////////////////////////////////////
//
// Image preprocessing.
//
// See "Modelling the image" in supplementary methods.
// The image is normalized to locally zero mean and globally unit standard
// deviation.

// Skip the mean removal step if this is set to 1. 
// This is really only for debugging. Do not change.
preprocess.skip=0

//Low pass filter used for mean removal has has this sigma
preprocess.lpf=5



//////////////////////////////////////////////////
//
// Initial spot placement.
//

//Options are: 
//  uniform (place spots uniformly over the area of interest)
//  intensity_sampled  (place spots more densely in brighter regions)
//intensity_sampled generally leads to slightly faster convergence.
placement=intensity_sampled



////////////////////////////////////////////////////////////////////////////////
//
// Things after here do not do anything.
//
// Things after here have no effect in the plugin, but are required if
// this config file is to be used in the standalone program
//

//Instead of calculating the scaling of the initial image to set the
//standard deviation to 1, use a fixed scaling. This is for debugging
//purposes and is very unlikely to be useful otherwise.
preprocess.fixed_scaling=0

//Threshold the log_ratios image at this level in order to find
//regions for analysis.
threshold=0

//Dilate regions found by thresholding by this radius.
radius=0

//Analyse marked region number 19:
cluster_to_show=19

//If this is set to 1, cluster_to_show is ignored and the largest
//region is used instead.
use_largest=1
Generated on Wed Nov 28 2012 15:39:12 for ThreeB by  doxygen 1.7.4